排序算法
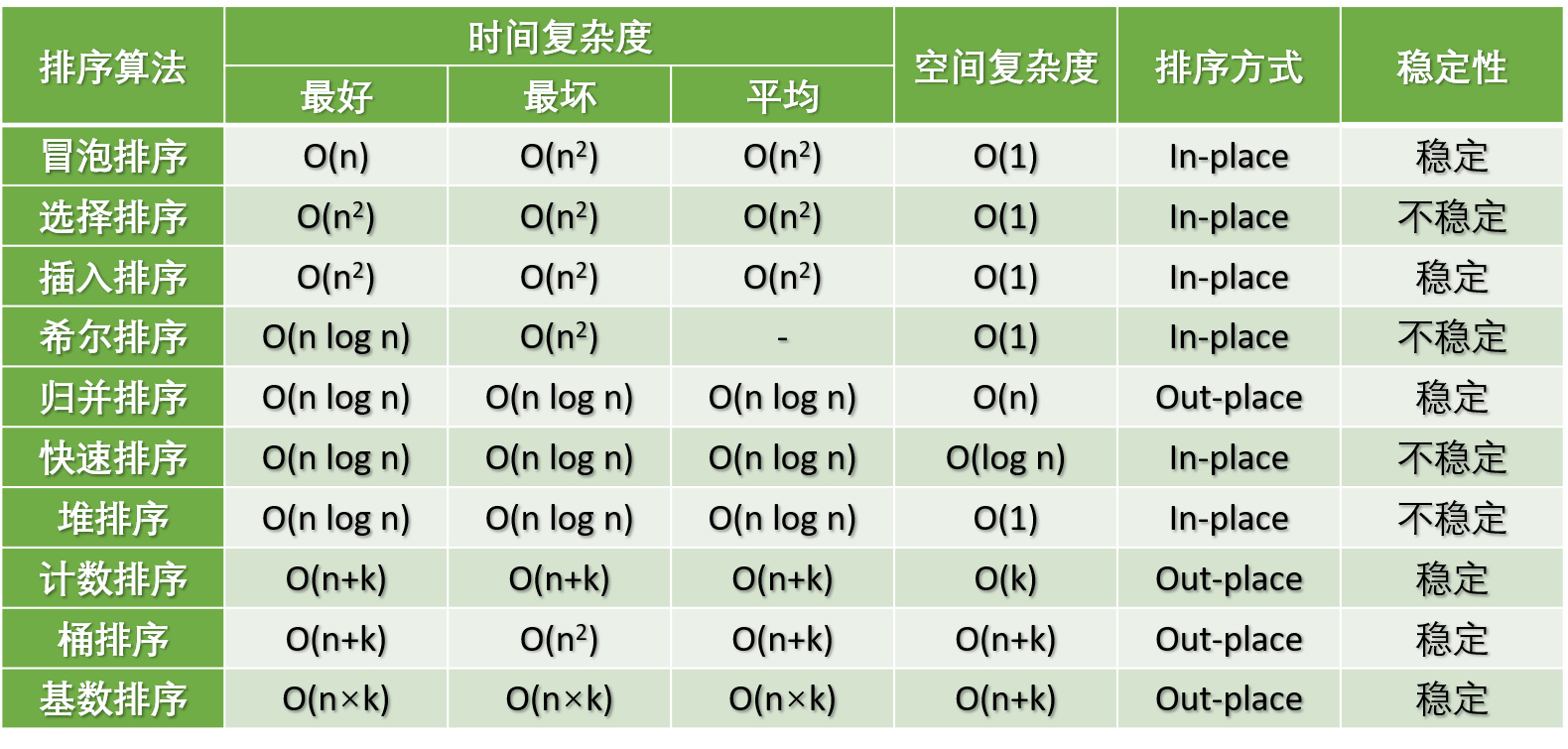
排序算法对比
快排最坏时间复杂度为O(n^2)。 最坏情况发生在待排序序列已经有序或基本有序的情况下。
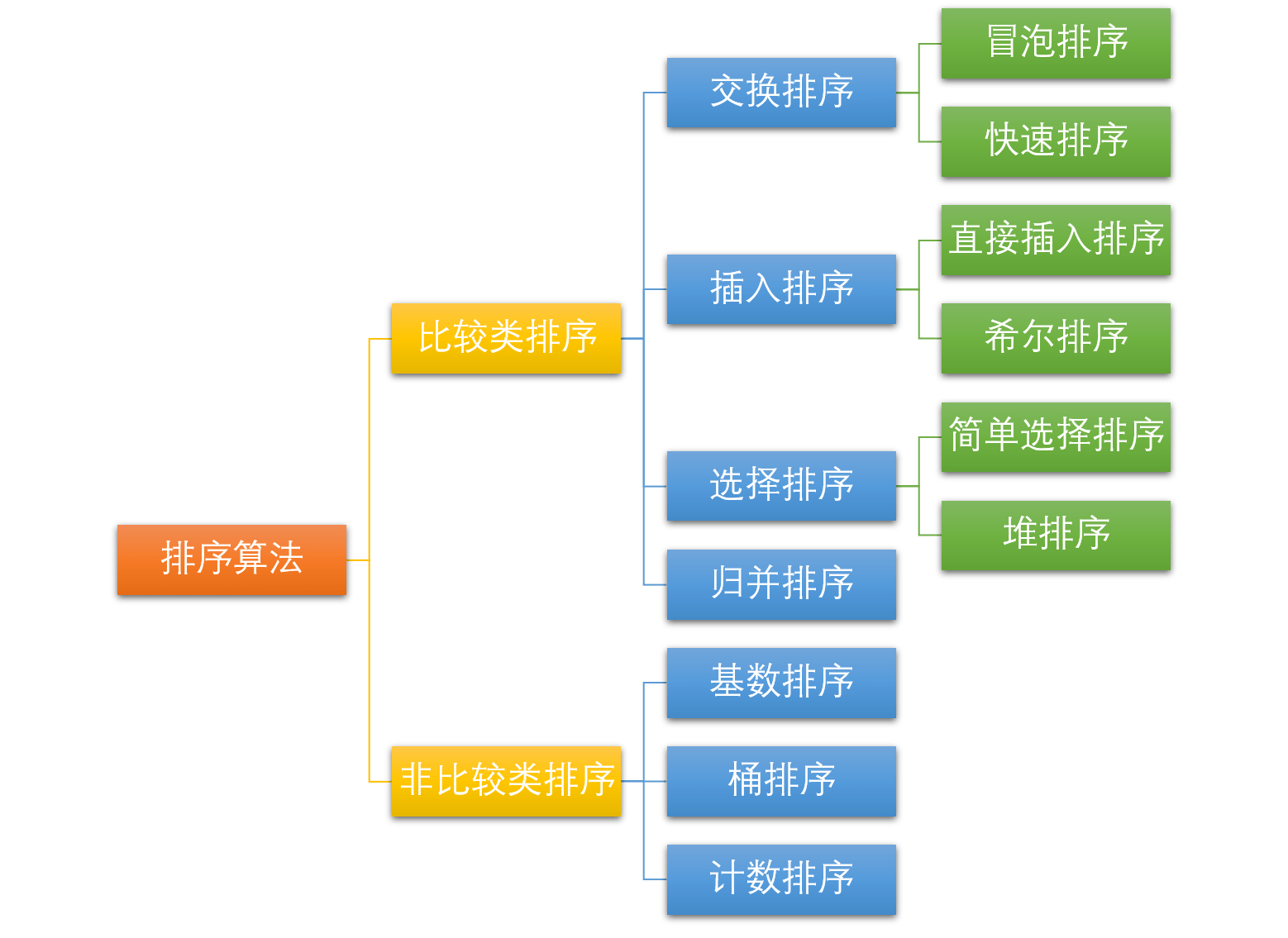
分类:
位图排序解决海量数据排序问题
位图排序的思想非常简单,那就是将一个个数据映射到它在有序的数轴上的一点,这个数轴可以是一个数组,数字的大小就是哈希因子,所以在遍历一遍数据集,设置好这些数字的点表示之后,我们就可以根据相应位置的状态,反过来来确定数据集中是否有这个数字,由于我们是有序的遍历的,因此查找出来的数字也是有序的,这样间接地达到了我们的目的。
位图很像数学中的数轴的概念,有哪些数字,就会在相应的位置标记它们,最后数据都是有序的。而且这种方法,一个数字占用的位置只有一个bit,对于0~2«32的4字节非负整数范围来说,最大的数为42亿,在实际应用场景下基本足够,而所需要的空间占用大概只需要2«32/8/1024^2=512M的内存,在内存占用上和效率上都有着无可比拟的优势。
- 位图排序是一种非比较排序算法,通常用于对整数进行排序。
- 它的基本思想是利用位图数据结构,将待排序的整数作为位图的索引,通过设置或清除位图中的相应位来表示整数的出现与否,从而实现排序。
- 位图排序适用于待排序整数范围不大的情况,因为位图需要的空间与待排序整数的最大值有关。
- 实现简单,时间复杂度为 O(n),但是需要较大的空间来存储位图。
例子:
|
|
获取一亿数据获取前100个最大值
局部淘汰法
1. 思路
最极端时K为1,那么我们可以自己实现max函数找到序列最小值,时间复杂度为 O(n) ,空间复杂度为 O(1) 。当K大于等于2时,我们需要维护一个长度为K的序列来保存最大的K个数,具体思路如下:
- step1:使用一个数组存储文件前100个浮点数,并排好序,记为序列L
- step2:遍历文件中剩余的数字,如果比序列L中最小值还要小则直接丢弃,否则通过插入排序的方式插入序列L并删掉最小数,最终得到的序列L就是前100大的数
2. 复杂度
- 时间复杂度:最坏情况下文件中每个数都需要遍历一遍序列L找到插入的位置,复杂度为 O(n×k) ;最好情况下一开始选择的100个数就是最大的,复杂度为 O(n)
- 空间复杂度:所用空间就是序列L的长度,即 O(k)
继续优化:以小顶堆的方式来维护序列L,具体看后面的思路四。
分治法
1. 思路
将数据分散成多份,通过多台机器分布式运算或者多线程并发计算的方式取得每份数据的Top K,然后汇总结果。
2. 优点
可以解决快速排序等思路中对计算机内存要求较大的问题。
小顶堆
1. 思路
取文件中前K个数在内存中维护一个长度为K的小顶堆,然后从文件中挨个读取数字并和堆顶比较,如果比堆顶小则直接丢弃,否则替换堆顶后调整小顶堆。遍历完文件中所有的数字后,小顶堆中的K个数就是所求的Top K。
2. 优点
只需要遍历一次文件中的数字,不存在多次读写数据的问题。
3. 复杂度
- 时间复杂度:最好情况下文件中前K个数就是Top K,遍历一遍文件即可,时间复杂度为 O(n) ;最坏情况下遍历文件中每个数都需要调整小顶堆,时间复杂度为 O(nlog2k)
- 空间复杂度:只需要在内存中维护小顶堆,空间复杂度为 O(k)
实际情况
实际处理大数据Top K问题时,需要考虑两个问题:
- 是否并发:并发可以显著提高运行速度,单机多核可以使用Hash将数据划分为多份子数据然后多线程并发排序,多机可以使用Hash+Socket方法将数据分发到多台机器上
- 是否有足够内存:如果机器内存足够可以直接在内存中使用Hash对数据进行切分,如果机器内存不足可以将原始文件切分成多个小文件
变式
1. 从十亿数据中找到出现次数最多的十个数字
用hash树记录每个数字出现的频率,转化为在各个数字的频率中找到Top K的问题。
2. 从十亿数据中找到升序的第七亿个数
2.1 快速排序
-
step1:以数组最后一个元素作为基准值,将数据partition为
[left,mid-1]和[mid,right]两个区间,其中[left,mid-1]的数都小于base值,[mid,right]都大于等于base值 -
step2:计算
[mid, right]数组长度L: -
- 如果L等于三亿,那么
[left,mid-1]中的七亿个数字小于[mid,right]中的三亿个数字,只需要在[left,mid-1]中找到最大值即可 - 如果L大于三亿,则将问题转化为在
[mid, right]中找到第(L-三亿)个数 - 如果L小于三亿则问题还是在
[left,mid-1]中找到第七亿大的数
- 如果L等于三亿,那么
在step2中,如果数据量级足够小则可以直接进行排序得到答案。
2.2 桶排序
假如数据的范围是有限的(有最大值和最小值)且较均匀分布,那么使用桶排序可以进一步提升效率:
- step1:获取数据的max和min
- step2:将所有的n份数据分到m个文件中,同时记录每份子文件中的数据量
- step3:从小到大累加文件数据量,找到第七亿个数所在的文件,记录前面文件的总数据量count
- step4:将问题转化为在第七亿个数所在的文件中寻找第(七亿-count)个数
在step4中,如果内存足够存放所有数据,可以直接排序获取第七亿个数字。
3. 对十亿数据进行排序
多路归并排序。